Capítulo 2 - Bits, Bytes y Binario
Un uno o un cero pueden no significar mucho para usted, pero para un computador significan mucho. Los números binarios, como usted ya sabe, son números compuestos únicamente de unos y ceros. Y son el único tipo de números que un computador puede entender. Un computador, o en todo caso, un computador digital (su Atari lo es), tiene grandes dificultades para entender conceptos poco claros. Para un computador, un interruptor está encendido o está apagado. Una señal eléctrica está presente o no lo está. Cada cosa en la pequeña mente de un microcomputador es blanco o negro, positivo o negativo, encendido o apagado.Llámelo como quiera. No importa. Ya sea masculino y femenino, Shiva y Shakti, o el yin y el yang. A veces los matemáticos la llaman el álgebra de Boole. Los diseñadores de computadores a veces la llaman lógica de dos estados. Y los programadores a menudo se refieren a ella como el sistema binario. En el sistema binario, el dígito 1 simboliza lo positivo, una corriente que fluye, por ejemplo, o un interruptor que está encendido. El dígito 0 representa lo negativo, una corriente que no fluye, o un interruptor que está apagado. Pero no hay dígito para el número 2. La única manera de representar el número 2 en binario es tomar un 1, moverlo un espacio a la izquierda, y poner a continuación un 0, de esta manera: 10. Eso es lo correcto. En notación binaria, «10» significa 2, no 10, «11» significa 3, «100» es 4, «101» es 5, y «110» es 6, y así sucesivamente.
Matemáticas Pingüinas
Si los números binarios lo frustran, un curso de Matemáticas Pingüinas el ayudara. Imagínese que usted es un pingüino, viviendo en un campo de hielo. Los pingüinos no tienen 10 dedos en cada mano, como los tiene la gente. En cambio, tienen dos aletas. Así que si usted fuera un pingüino, y contara sus aletas tal como algunas personas cuentan sus dedos, usted sería capaz de contar sólo hasta 2. Sin embargo, si usted fuera un pingüino muy brillante, es posible que un día descifre cómo usar sus aletas para contar más allá de 2. Supongamos, por ejemplo, que se decidió a definir que la aleta derecha levantada es igual a 1, y que aleta izquierda levantada es igual a 2, entonces usted puede decir que las dos aletas levantadas equivalen a 3. Ahora supongamos que usted fuera un pingüino extraordinariamente brillante, y diseñó un sistema de notación para expresar por escrito lo que ha descubierto. Usted podría utilizar un 0 para representar a ninguna aleta levantada, y un 1 para representar una aleta levantada. Y entonces usted podría escribir estas ecuaciones en el hielo:
Números Pingüinos
00 = 0 01 = 1 10 = 2 11 = 3

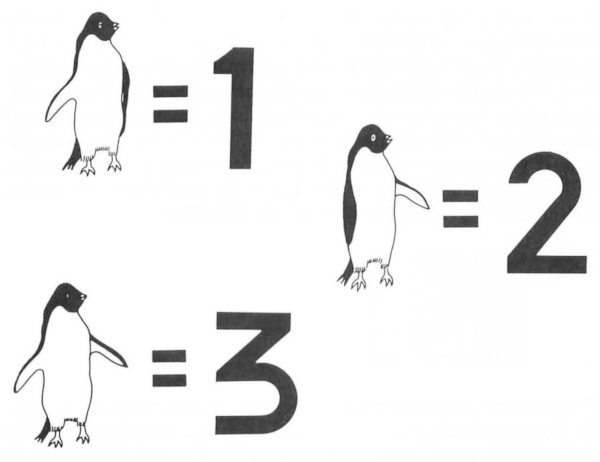
Estos, por supuesto, son números binarios. Y lo que muestran, en Matemáticas Pingüinas, es que se pueden expresar cuatro valores – del 0 al 3 – como números binarios de 2-bits (dos dígitos). Ahora vamos a suponer que usted, como pingüino, quiere aprender a contar más allá del 3. Imaginemos que usted miró sus pies y se dio cuenta que tenía dos aletas más. ¡Voilá, números más grandes! Si usted se sentara en su campo de hielo de modo que usted pudiera levantar ambos brazos y ambas piernas al mismo tiempo, usted puede contar de la siguiente manera:
0000 = 0 0001 = 1 0010 = 2 0011 = 3 0100 = 4 0101 = 5 0110 = 6 0111 = 7 1000 = 8 1001 = 9
... y así sucesivamente.
Si sigue contando así finalmente descubriría que puede expresar 16 valores, del 0 al 15, usando números de 4 bits. Sólo queda una lección más de Matemáticas Pingüinas. Imagine que usted, como buen pingüino, se ha casado con una pingüina. Y, utilizando su habilidad con los números binarios, determinó que entre usted y su pareja hacen un total de ocho aletas. Si su pareja decide cooperar con usted y contar también con sus aletas, los dos ahora podrían sentarse en el hielo y comenzar un paseo en témpano con números que se verían de la siguiente manera:
0000 0001 = 1 0000 0010 = 2 0000 0011 = 3 0000 0100 = 4 0000 0101 = 5
Si usted y su pareja siguieran contando de esta manera, mediante Matemáticas Pingüinas de 8 bits (aletas), finalmente descubriría que con ocho aletas se puede contar desde 0 hasta 255, lo que da un total de 256 valores. Esto completa nuestro breve curso en Matemáticas Pingüinas. Lo que nos ha enseñado es que es posible expresar 256 valores, del 0 a 255, usando números binarios de 8 bits.
Bits, Bytes y Nibble
Como se ha señalado unos párrafos atrás, cuando unos y ceros se usan para expresar números binarios, se les llaman bits. Un grupo de ocho bits se llama byte. Y un grupo de cuatro bits se llama nibble (a veces se escribe «nybble»). Y un grupo de 16 bits se le denomina palabra (word). Ahora vamos a echar otro vistazo a una serie de bytes de 8 bits. Obsérvelos de cerca, y verá que cada número binario que termina en cero es dos veces mayor que el número anterior, o en otras palabras, es el cuadrado del número anterior:
0000 0001 = 1 0000 0010 = 2 0000 0100 = 4 0000 1000 = 8 0001 0000 = 16 0010 0000 = 32 0100 0000 = 64 1000 0000 = 128
Acá hay dos números binarios más que los programadores de lenguaje ensamblador a menudo encuentran útil memorizarlos:
1111 1111 = 255 1111 1111 1111 1111 = 65,535
El número 255 es digno de mención porque es el número de 8 bits más grande. El número 65.535 es el número de 16 bits más grande. Ahora la trama se complica. Como ya hemos mencionado, los computadores Atari se llaman computadores de 8 bits porque están construidos alrededor de un microprocesador de 8 bits, un procesador de computadores que maneja números binarios de hasta sólo ocho posiciones de largo. Debido a esta limitación, el Atari no puede realizar cálculos con números mayores a 255, de hecho... ¡Ni siquiera puede realizar un cálculo cuyo resultado sea mayor a 255!
Obviamente, esta limitación de los 8-bits impone severas restricciones sobre la capacidad de los computadores Atari para realizar cálculos con números grandes. En efecto, la Unidad Aritmética Lógica (Arithmetic Logic Unit – ALU) del 6502 es como una calculadora que no puede manejar un número mayor a 255. Hay maneras de eludir esta limitación, por supuesto, pero no es fácil. Para trabajar con números de más de 255, un computador de 8 bits tiene que realizar una serie más compleja de las operaciones. Si un número es mayor que 255, un computador de 8 bits tiene que dividirlo en trozos 8-bits, y realizar cada cálculo requerido en cada número de 8 bits. Luego, el computador tiene que juntar todos estos números de 8 bits.
Si el resultado de un cálculo tiene más de ocho bits de largo, las cosas se complican aún más. Esto porque cada posición de memoria en un computador de 8 bits, cada celda en su memoria de acceso aleatorio (RAM), así como su memoria de sólo lectura (ROM), es un registro de memoria de 8 bits. Así que si desea almacenar un número mayor que 255 en la memoria de un computador de 8-bits, usted tiene que dividirlo en dos o más números de 8 bits, y después almacenar cada uno de estos números en un lugar de memoria independiente. Y después, si alguna vez desea utilizar el número original de nuevo, tiene que juntar cada uno de los trozos de 8 bits en que fue dividido anteriormente.
Computadores de 8-bits versus 16-bits
Ahora que sabe todo eso, podrá entender por qué los computadores de 16 bits, como los computadores personales IBM y sus compatibles, pueden correr más rápido que los computadores de 8 bits. Un equipo de 16 bits puede manejar números binarios de 16 bits de largo, sin hacer operaciones matemáticas cortando y pegando números, y por lo tanto pueden procesar números que llegan hasta el 65.535 en trozos individuales, una palabra de 16 bits a la vez. Así que los computadores de 16 bits son considerablemente más rápidos que los de 8 bits, por lo menos cuando están operando con números grandes. Los computadores de 16 bits también tienen otra ventaja sobre los de 8 bits. Pueden estar al tanto de mucha más información simultánea que los computadores de 8 bits. Y por lo tanto, puede ser equipado con memorias mucho más grandes.
Mapa de Memoria de su Computador
La memoria de un computador puede ser visualizada como una cuadrícula grande que contiene miles de casillas, o posiciones de memoria. En un computador Atari, cada uno de estas posiciones puede contener un número de 8 bits. Anteriormente, se presentó una analogía entre la memoria de un computador y las filas sobre filas de casillas de correos. Ahora podemos ampliar esa analogía un poco más.
Como hemos mencionado, cada posición de memoria en su computador tiene una dirección de memoria individual y única. Y cada una de estas direcciones está en realidad compuesta de dos números índice. El primero de estos números se podría llamar el eje X de la posición de la dirección en la matriz de memoria de su computador. El segundo número se podría llamar el eje Y de la posición. Al utilizar este sistema de coordenadas X, Y para localizar las direcciones en su memoria, el computador Atari puede estar al tanto de las direcciones que tienen hasta 16 bits de largo, aunque sólo se trate de un computador de 8-bits. Todo lo que tiene que hacer es almacenar el eje X en un registro de 8 bits y el eje Y en otro registro de 8 bits. Así que cuando usted quiera que su Atari busque un trozo de información de su memoria, todo lo que tienes que hacer es indicar cuál es el eje X y el eje Y de la dirección donde están los datos. Así el computador puede encontrar inmediatamente los datos que usted está buscando.
La Libreta de Direcciones de su Computador
Pero aun así hay un límite en el número de posiciones de direcciones que un computador de 8 bits puede estar al tanto. Dado que 255 es el número más grande que un registro de 8 bits puede almacenar, el eje X de una dirección puede ir sólo de 0 a 255, o sea un total de 256 números. El mismo límite se aplica al eje Y. Así que a menos que se utilicen elaborados trucos de expansión de memoria, la capacidad máxima de un computador de 8 bits es 256 veces 256, o sea 65.536, es decir, 64K de memoria. La razón de este número, por cierto, es que 64 K equivale a un número binario, no un a número decimal. 64K no es igual a 64 multiplicado por 1.000, en cambio equivale al producto de 64 y 1024.
Los dos números cuando están escritos en notación decimal pareciera que fueron obtenidos como por arte de magia, pero en binario ambos son números redondos: 0100 000 y 0100 000 000, respectivamente.
La Diferencia Que Hacen los 8 Bits
Si un computador de 16-bits está al tanto de las direcciones en su memoria de la misma manera que un computador de 8-bits, utilizando el eje X y el eje Y de cada posición como puntos de referencia, entonces un equipo de 16 bits puede direccionar más de 4 millones de posiciones de memoria (65.536 celdas por 65.536 celdas). Sin embargo, los computadores de 16-bits no suelen estar al tanto de la dirección en memoria de esa manera. En el IBM-PC, por ejemplo, a cada posición de memoria se le asigna lo que equivale a una dirección de 20 bits. Así, un IBM-PC puede direccionar 1.048.576 posiciones; no son exactamente los más de 4 millones de posiciones que podría abordar con el sistema de la matriz X, Y, pero aún suficientes posiciones para almacenar más de un millón de bytes (un megabyte) de memoria.
Ahora puede entender de qué se trata todo este alboroto acerca de los computadores de 16 bits. Pueden direccionar más memoria que los computadores de 8 bits, y también pueden procesar información más rápido. Además, son más fáciles de programar en lenguaje ensamblador que los computadores de 8-bits, ya que pueden manipular de manera natural fragmentos de datos de 16 bits de longitud. Dado que los computadores Atari son de 8 bits, nada de esto aplicable a los computadores de 16 bits será de mucha ayuda en su búsqueda de conocimientos sobre el lenguaje ensamblador de Atari. Afortunadamente, sin embargo, un conocimiento del lenguaje ensamblador de Atari le ayudará mucho si alguna vez decide estudiar lenguaje ensamblador de 16-bits. Si aprende a jugar con bits lo suficientemente bien como para convertirse en un buen programador de lenguaje ensamblador de Atari, probablemente será más rápido aprender el lenguaje ensamblador de 16-bits, ya que éste no requiere acoplar números de 8 bits.
El Sistema Numérico Hexadecimal
¿Cuál es la suma de D más F? Bueno, es 1C, si usted está trabajando en números hexadecimales.
Los números hexadecimales, como puede saberlo si usted ha trabajado mucho programando, son extrañas combinaciones de letras y números que se utilizan a menudo en programas en lenguaje ensamblador. El sistema de notación hexadecimal utiliza no sólo los dígitos del 0 al 9, sino también las letras A a la F. Así que combinaciones de letras y números de tan extraño aspecto como FC3B, 4A5D e incluso ABCD son números perfectamente válidos en el sistema hexadecimal. Los números hexadecimales son utilizados a menudo por los programadores en lenguaje ensamblador, ya que están muy relacionados con los números binarios. A continuación echaremos un vistazo a esta estrecha relación.
Matemáticas con 16 Dedos
¿Recuerda cómo usamos las Matemáticas Pingüinas para explicar el concepto de números binarios? Bueno, si puede imaginar que vive en una sociedad donde cada individuo tiene 16 dedos en vez de 10 como nosotros, o dos aletas como un pingüino, entonces será capaz de comprender el concepto de números hexadecimales con bastante facilidad. Los números binarios, como hemos señalado, tienen base 2.
Los números decimales, del tipo que estamos acostumbrados, tienen base 10. Y los números hexadecimales tienen base 16. Los números hexadecimales se utilizan en la programación en lenguaje ensamblador, porque son muy similares a los números binarios, lo cual, como hemos señalado en el Capítulo 1, son el tipo de números que entienden los computadores. A primera vista, puede ser difícil ver qué tienen en común los números binarios y los hexadecimales. Pero vera claramente cómo los números binarios y hexadecimales se relacionan entre sí, mirando este gráfico:
| Decimal | Hexadecimal | Binario |
|---|---|---|
| 1 | 1 | 0000 0001 |
| 2 | 2 | 0000 0010 |
| 3 | 3 | 0000 0011 |
| 4 | 4 | 0000 0100 |
| 5 | 5 | 0000 0101 |
| 6 | 6 | 0000 0110 |
| 7 | 7 | 0000 0111 |
| 8 | 8 | 0000 1000 |
| 9 | 9 | 0000 1001 |
| 10 | A | 0000 1010 |
| 11 | B | 0000 1011 |
| 12 | C | 0000 1100 |
| 13 | D | 0000 1101 |
| 14 | E | 0000 1110 |
| 15 | F | 0000 1111 |
| 16 | 10 | 0001 0000 |
Como puede ver en esta lista, el número decimal 16 se escribe «10» en hexadecimal y «0001 0000» en binario, y es por tanto un número redondo en ambos sistemas. Y el dígito hexadecimal F, que viene justo antes del 10 hexadecimal (o 16 decimal), se escribe en binario 00001111. A medida que se familiarice con los sistemas binario y hexadecimal, comenzará a notar muchas otras similitudes entre ellos. Por ejemplo, el número decimal 255 (el mayor número de 8 bits) es 1111 1111 en binario y FF en hexadecimal. El número decimal 65.535 (la dirección de memoria más alta en un equipo de 64K) se escribe FFFF en hexadecimal y 1111 1111 1111 1111 en binario. Y así sucesivamente. El punto de todo esto es que es mucho más fácil de convertir entre números binarios y hexadecimales, que convertir entre números binarios y decimales.
1011 1000 Binario B 8 Hexadecimal 184 Decimal 0010 1110 Binario 2 E Hexadecimal 46 Decimal 1111 1100 Binario F C Hexadecimal 252 Decimal 0001 1100 Binario 1 C Hexadecimal 28 Decimal
Como puede ver, un nibble (cuatro bits) en notación binaria siempre equivale a un dígito en notación hexadecimal. Pero no hay ninguna relación clara entre el largo de un número binario y el largo del mismo número escrito en notación decimal. Este mismo principio puede extenderse a conversiones de binario, hexadecimal y decimal de números de 16 bits. Por ejemplo:
1111 1100 0001 1100 Binario F C 1 C Hexadecimal 64540 Decimal
Algunos programas ilustrativos
Ahora vamos a mirar algunos programas básicos que llevan a cabo operaciones con números binarios, decimales y hexadecimales. Dado que todos los computadores Atari son computadores de 8 bits (al momento de la escritura de este libro, de todos modos), la única forma de almacenar un número de 16 bits en un Atari es ponerlo en dos registros de la memoria. Y los computadores basados en el 6502 usan la rara convención (para algunas personas) de almacenar números de 16 bits de la siguiente manera: primero el byte más bajo (menos significativo) y luego el byte más alto (más significativo). Por ejemplo, si el número hexadecimal FC1C va a ser almacenado en las direcciones de memoria hexadecimal 0600 y 0601, FC (el byte más significativo) se almacenará en la dirección 0601, y 1C (el byte menos significativo) se almacenará en la dirección 0600. (En programas en lenguaje ensamblador, por cierto, los números hexadecimales suelen ir precedidas signos de dólar ($) para que puedan distinguirse de los números decimales. Por lo tanto, en un programa de lenguaje ensamblador, las direcciones hexadecimales 0600 y 0601 se escriben $0600 y $0601.
Ahora vamos a suponer, sólo para fines ilustrativos, que usted necesita almacenar un número de 16 bits en dos direcciones de 8 bytes en la memoria RAM del computador ($0600 y $0601 por ejemplo), mientras ejecuta un programa en Basic. Dado que los programas en BASIC se escriben con números decimales ordinarios, lo primero que habría que hacer es convertir las direcciones con las que se va a trabajar, $0600 y $0601, en números decimales. Usted puede hacer esto de distintas maneras. Puede buscar los equivalentes decimales de $0600 y $0601 en una tabla de conversión decimal / hexadecimal. O también puede calcular las conversiones necesarias a mano. O también podría realizarlas con la ayuda de un programa. No importa cómo se las arregló para hacer las conversiones. Sin embargo, lo que acabaría descubriendo es que el número hexadecimal $0601 equivale al decimal 1537. Una vez que lo deduzca, podrá almacenar el valor de 16-bits en las direcciones $0600 y $0601 utilizando la siguiente rutina en Basic:
Rutina para almacenar números de 16 bits en la RAM
10 PRINT "INGRESE UN ENTERO POSITIVO" 20 PRINT "DE 0 A 65.535" 30 INPUT X 40 LET HIBYTE=INT(X/256) 50 LET LOBYTE=X-HIBYTE*256 60 POKE 1536,LOBYTE 70 POKE 1537,HIBYTE 80 END
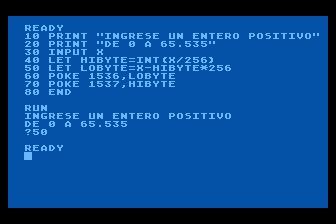
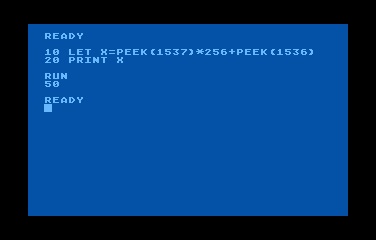
Ahora supongamos que usted quiere recuperar un número de 16 bits almacenado en la memoria RAM de su computador; por ejemplo, el número almacenado en la memoria de las direcciones $0600 y $0601 en el programa anterior. Y supongamos una vez más, que quería hacer eso, mientras se ejecuta un programa en BASIC. Su rutina podría ser algo como esto:
Recuperación de números de 16 bits desde la RAM
10 LET X=PEEK(1537)*256+PEEK(1536) 20 PRINT X
Conversión de números binarios a números decimales
Dado que los programadores de lenguaje ensamblador trabajan con tres diferentes tipos de números (decimal, hexadecimal y binario), a menudo se encuentran con que es necesario realizar conversiones entre una base numérica y otra. No es muy difícil de convertir un número binario a un número decimal. En un número binario, el bit más a la derecha representa 2 a la potencia de 0. El siguiente bit a la izquierda representa 2 a la potencia de 1, el siguiente representa 2 a la potencia de 2, y así sucesivamente. Los dígitos en un número binario de 8 bits se numeran del 0 al 7, partiendo desde el dígito de más a la derecha. A menudo se refiere al bit de más a la derecha como el menos importante (o LSB – Least Significant Bit). Representa el 2 a la potencia de 0, o sea, el número 1. Y el bit más a la izquierda – a menudo llamado el bit más significativo (o MSB – Most Significant Bit) – es igual a 2 a la potencia de 7, o sea, 128. He aquí una lista de ecuaciones simples que ilustran lo que cada bit en un número binario de 8 bits significa:
Bit 0 = 2^0 = 1 Bit 1 = 2^1 = 2 Bit 2 = 2^2 = 4 Bit 3 = 2^3 = 8 Bit 4 = 2^4 = 16 Bit 5 = 2^5 = 32 Bit 6 = 2^6 = 64 Bit 7 = 2^7 = 128
Utilizando la tabla de arriba, es fácil convertir cualquier número binario de 8 bits a su equivalente decimal. En lugar de escribir el número de abajo, de izquierda a derecha, escríbalo en una columna vertical, con el bit 0 en la parte superior de la columna y el bit 7 en la parte inferior. Luego se multiplican cada bit del número binario por el número decimal que representa. Luego sume el resultado de todas estas multiplicaciones. El total que se obtiene es el valor decimal del número binario. Supongamos, por ejemplo, que quiere convertir el número binario 00101001 en un número decimal. Aquí le mostramos cómo hacerlo:
1 X 1 = 1 0 X 2 = 0 0 X 4 = 0 1 X 8 = 8 0 X 16 = 0 1 X 32 = 32 0 X 64 = 0 0 X 128 = 0 ________________ TOTAL = 41
Según los resultados de este cálculo, el número binario 00101001 equivale al número decimal 41. Busque 00101001 o 41 en una tabla de conversión de binario a decimal o de decimal a binario, y verá que el cálculo es exacto. Y esta técnica de conversión funcionará con cualquier otro número binario. Ahora vamos a ir en la dirección contraria, y convertiremos un número decimal a binario. Y aquí está cómo lo haremos: Vamos a dividir el número por 2, y anotamos el cociente y el resto. Ya que se divide por 2, el cociente será un 1 o un 0. Así que vamos a escribir un 1 o un 0, según sea el caso. Luego tomaremos el cociente que tenemos, lo dividimos por dos, y escribimos el cociente abajo. Si hay un resto (un 1 o un 0), lo escribimos, también, justo debajo del primer resto. Cuando no queden más números que dividir, vamos a escribir todos los restos que tenemos, leyendo desde abajo hacia arriba. Lo que obtendremos entonces, por supuesto, es un número binario, un número compuesto de unos y ceros. Y ese número será el equivalente binario del número decimal con el que empezamos. Ahora vamos a probar esta técnica de conversión con el número decimal 117:
117/2 = 58 con resto 1 58/2 = 29 con resto 0 29/2 = 14 con resto 1 14/2 = 7 con resto 0 7/2 = 3 con resto 1 3/2 = 1 con resto 1 1/2 = 0 con resto 1
Según los resultados de este cálculo, el equivalente binario del número decimal 117 es 01110101. Y este resultado, como lo puede comprobar con una tabla de conversión de decimal a binario, también es correcto.
Conversiones De binario a Hexadecimal y de Hexadecimal a Binario
Es muy fácil convertir números binarios a sus equivalentes hexadecimales. Sólo tiene que utilizar esta tabla:
| HEXADECIMAL | BINARIO |
|---|---|
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
Para convertir un número hexadecimal de varios dígitos a binario, tome los dígitos hexadecimales y conviértalos cada uno por separado. Por ejemplo, el equivalente binario del número hexadecimal C0 es 1100 0000. El equivalente binario del número hexadecimal 8f2 es 1000 1111 0010. El binario equivalente al número hexadecimal 7A1B es 0111 1010 0001 1011. Y así sucesivamente. Para convertir los números binarios a números hexadecimales, utilice la tabla a la inversa. El número binario 1101 0110 1110 0101, por ejemplo, es equivalente al número hexadecimal D6E5.
Haciéndolo de la manera fácil
Aunque no es difícil convertir números binarios a hexadecimal y viceversa, lleva mucho tiempo hacerlo a mano, y cuando se programa en lenguaje ensamblador, tiene que hacer un montón de conversiones de binario a decimal y decimal a binario. Así que hay un montón de programas en BASIC para convertir números entre los sistemas de notación binaria y decimal. Y ahora le voy a regalar dos de ellos, absolutamente gratis. Aquí tiene uno para la conversión de números binarios a números decimales:
Conversión de Números Binarios a Números Decimales
10 DIM BN$(9),BIT(8),T$(1) 20 GRAPHICS 0 25 ? :? "CONVIERTE DE BINARIO A DECIMAL" 30 ? :? "ESCRIBE UN NUMERO BINARIO:":? :INPUT BN$ 35 IF LEN(BN$)<>8 THEN 30 40 FOR L=1 TO 8 50 T$=BN$(L) 55 IF T$<>"0" AND T$<>"1" THEN 30 60 BIT(L)=VAL(T$) 70 NEXT L 75 ANS=0 80 M=256 90 FOR X=1 TO 8 100 M=M/2:ANS=ANS+BIT(X)*M 110 NEXT X 140 ? "DECIMAL: ";ANS 150 GOTO 30
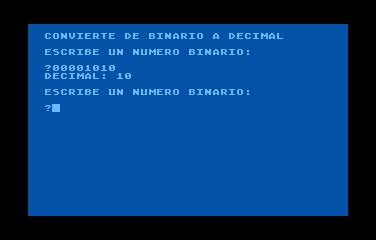
Y aquí hay un programa para la conversión de números decimales a números binarios:
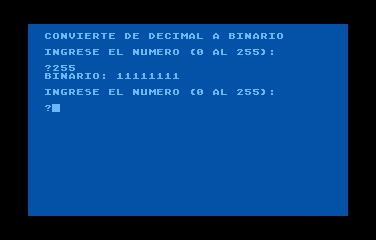
Conversión de Números Decimales a Números Binarios
10 DIM BIN$(8),TEMP$(8),R$(1) 20 GRAPHICS 0 30 ? :? "CONVIERTE DE DECIMAL A BINARIO" 40 ? :? "INGRESE EL NUMERO (0 AL 255):":? :TRAP 40:INPUT NR 50 IF NR-INT(NR)<>0 THEN 40 60 IF NR>255 OR NR<0 THEN 40 70 FOR L=1 TO 8 80 Q=NR/2 90 R=Q-INT(Q) 100 IF R=0 THEN R$="0":GOTO 120 110 R$="1" 120 TEMP$(1)=R$:TEMP$(2)=BIN$:BIN$=TEMP$ 130 NR=INT(Q) 140 NEXT L 150 ? "BINARIO: ";BIN$ 160 TRAP 40000 170 GOTO 40
Conversión de Decimal a Hexadecimal
La conversión de decimal a hexadecimal es un proceso complejo que es mejor realizarlo usando un computador o una calculadora especial. Texas Instruments ofrece una calculadora llamada The Programmer que puede realizar conversiones de decimal a hexadecimal en un segundo, y también puede sumar, restar, multiplicar y dividir ambos números decimales y hexadecimales. Muchos diseñadores de programadores en lenguaje ensamblador usan The Programmer de Texas Instruments (TI), o cualquier otra calculadora similar, y tienen dificultades para manejarse sin ella. En caso de que no pueda conseguir una calculadora de programadores ahora mismo, aquí hay un programa en BASIC de Atari que convierte números decimales a números hexadecimales y viceversa inversa. Hay otro programa está disponible en la página H-18 del manual de referencia BASIC que viene con su cartucho BASIC de Atari.
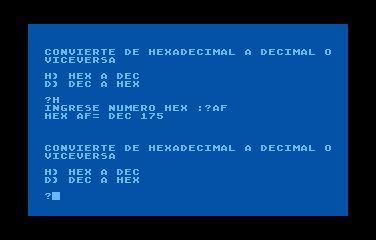
Programa para convertir de Decimal a Hexadecimal y de Hexadecimal a Decimal
10 REM 20 REM CONVIERTE DE HEXADECIMAL A DECIMAL O VICEVERSA ATARI ROOTS 30 REM 40 REM EL CAMINO RAPIDO 50 REM NO UTILICE MATEMATICAS 60 REM 70 DIM H$(40),A$(40) 80 REM 90 PRINT 100 PRINT 110 PRINT 120 PRINT "CONVIERTE DE HEXADECIMAL A DECIMAL O VICEVERSA" 130 PRINT 140 PRINT "H) HEX A DEC" 150 PRINT "D) DEC A HEX" 160 PRINT 180 INPUT A$ 190 IF A$="H" THEN 220 200 IF A$="D" THEN 400 210 GOTO 100 220 REM 230 REM CONVIERTE DE HEXADECIMAL A DECIMAL 240 REM 250 PRINT "INGRESE NUMERO HEX :"; 260 INPUT H$ 270 REM 280 D=0 290 S=1:REM MULTIPLICADOR POSICIONAL 295 REM PASAR POR LA CADENA 300 FOR L=LEN(H$) TO 1 STEP -1 310 A$=H$(L,L) 320 REM 330 REM CONVIERTE "0"-"F" A 0-15 340 N=ASC(A$)-48:IF N>9 THEN N=N-7 345 IF N<0 OR N>15 THEN 90 350 D=D+N*S 360 S=S*16 370 NEXT L 380 PRINT "HEX ";H$;"= DEC ";D 390 GOTO 90 400 REM 410 REM CONVIERTE DE DECIMAL A HEXADECIMAL 420 REM 430 PRINT "INGRESE NUMERO DEC :"; 440 INPUT D 450 REM 460 REM EN PRIMER LUGAR ENCONTRAMOS EL DIGITO MAS ALTO 470 REM 480 S=16 490 X=2 500 IF S<D THEN X=X+1:S=S*16:GOTO 500 505 PRINT "DECIMAL ";D;" = HEX "; 510 T=D 520 FOR L=X TO 1 STEP -1 530 N=INT(T/S) 540 PRINT CHR$(48+N+7*(N>9));:REM CONVIERTE DEC A HEX 0-F 550 T=T-N*S:S=S/16 560 NEXT L 570 PRINT 580 GOTO 90
Así concluye nuestro curso intensivo en bits, bytes y números binarios. Este fue un capítulo importante porque es un requisito previo para el capítulo 3, que a su vez es un requisito previo para el capítulo 4, donde tendré la oportunidad de realmente comenzar a escribir algunos programas en lenguaje ensamblador.
Algo para progresar
Mientras tanto, aquí hay otro programa BASIC que puede ayudarle a sentir que se está comunicando con su Atari. Utiliza un bucle infinito para recorrer todos los colores y matices que su computador puede generar, cargando cada uno de ellos en el registro de memoria que controla la zona del borde de la pantalla de video. En el capítulo 9, Programando Bit a Bit, aprenderá cómo hacer esto mismo truco utilizando el lenguaje ensamblador.
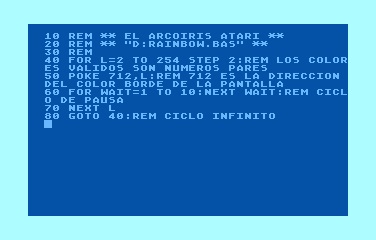
PROGRAMA DE EJEMPLO N°2
El Arcoíris ATARI
10 REM ** EL ARCOIRIS ATARI ** 20 REM ** "D:RAINBOW.BAS" ** 30 REM 40 FOR L=2 TO 254 STEP 2:REM LOS COLORES VALIDOS SON NUMEROS PARES 50 POKE 712,L:REM 712 ES LA DIRECCION DEL COLOR BORDE DE LA PANTALLA 60 FOR WAIT=1 TO 10:NEXT WAIT:REM CICLO DE PAUSA 70 NEXT L 80 GOTO 40:REM CICLO INFINITO
¡Digite este programa en su computador, ejecútelo, y disfrute el espectáculo! Luego seguiremos con el Capítulo 3.